Chapitre 11: Les amplificateurs opérationnels

L'amplificateur opérationnel occupe une place prépondérante dans l'électronique moderne. On le rencontre dans beaucoup d’applications linéaires mais aussi dans les alimentations. La connaissance de ses caractéristiques est importante.

• 1. Introduction
• 2. L'amplificateur opérationnel
• 3. Représentation
• 4. Ce que fait l'amplificateur opérationnel
• 5. Modèle simplifié
• 6. Différence entre un ampli idéal et un ampli réel
• 7. Circuits fondamentaux à ampli opérationnel
• 8. Ampli de courant pour ampli de tension
• Retour à semi-conducteurs
• Sommaire
• Accueil

1.      Introduction: 

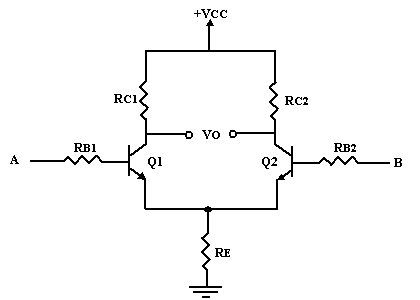
Tout amplificateur opérationnel que l'on notera AOP repose sur un circuit appelé amplificateur différentiel. Cet amplificateur a la particularité d'amplifier la différence des tensions appliquées sur les entrées A et B. On récupère le signal de sortie entre les deux collecteurs.

Raisonnons en continu. Si nous polarisons différemment notre entrée A de notre entrée B, nous aurons Ic1 différent de Ic2. Nous aurons une chute de tension différente sur le collecteur 1 de celle du collecteur 2 puisque le courant Ic1 sera différent de Ic2. Ceci implique que la ddp entre collecteurs sera bien l'image de la différence des tensions d'entrée. 

2.      L'amplificateur opérationnel :

Un AOP est constitué d’un amplificateur différentiel ayant une impédance d’entrée très élevée suivi d’un amplificateur en tension (montage émetteur commun) et d’un amplificateur en courant ayant une impédance de sortie très faible. Vous imaginerez donc sans peine qu'un amplificateur opérationnel est un peu plus complexe que la représentation simplifiée faite ci-dessus. Toutefois on ne montre jamais sur les schémas le détail du circuit utilisé, ce serait complexe et inutile. L'amplificateur, en fonction de la configuration qu'on lui donne, réalise une fonction. L'AOP n'est toutefois pas parfait, il a quelques petits défauts qu'il faut connaître.  

3.      Représentation :

Et voici le symbole, on trouve deux entrées : une, notée “+” appelée “entrée non inverseuse” et l'autre notée “-” est “l'entrée inverseuse”. Les connexions d'alimentation ne sont pas représentées. 

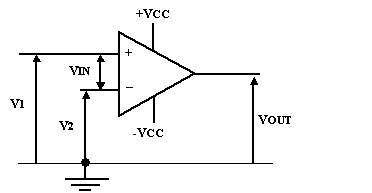
4.      Fondamentalement voilà ce que fait un AOP :

On alimente l'amplificateur avec une tension symétrique ou pas. On applique sur l'entrée non inverseuse une tension V1, et sur l'entrée inverseuse une tension V2. La tension résultante d'entrée, appelée VIN est égale à V1-V2. Cette tension VIN = (V1-V2) est amplifiée par le facteur d'amplification A de l'AOP qui est constant. On la retrouve à la sortie, elle s'appelle VOUT et est égale à VIN x A

5.      Modèle simplifié d’amplificateur opérationnel : 

• Les technologies

Bipolaire type UA741,

Fet, type TL072 l'entrée est constituée de transistors à effet de champ

Lin CMOS (Complementary metal oxide semiconductor) réalisée à partir de transistors MOS complémentaires. 

• Gain en boucle ouverte

Autour de 200 000 (UA741) 

• Courant maximum disponible

± 25 mA (UA741) 

• Bande passante

L'AOP qui est un dispositif à couplage direct passe le continu. Sa bande passante sans contre réaction va du continu à 1 MHz (UA741). 

• L'impédance d'entrée

Les AOP ont une grande impédance d'entrée, celle-ci est spécifiée par le constructeur pour chaque modèle. Pour un UA741 très classique comptez 2 MW. 

• Impédance de sortie

L'impédance de sortie est très basse. Elle se situe autour de 75 ohms pour le UA741. 

• L'alimentation en courant continu

Initialement les AOP étaient conçus pour fonctionner, alimentés par une tension symétrique +/-, mais on peut les faire fonctionner avec une seule tension même si ceci s'accompagne d'une perte de dynamique. 

           Caractéristiques de l’amplificateur opérationnel idéal

L’AOP sans circuit externe de contre réaction de la sortie vers l’entrée est décrit comme étant en boucle ouverte. En boucle ouverte, les caractéristiques de l’ampli opérationnel idéal sont les suivantes :

Gain différentiel = ∞ 

Impédance d’entrée = ∞ W

Impédance de sortie = 0 W

Bande passante = ∞ Hz

Gain en mode commun = 0

Tension de décalage = 0 volt 

Nécessité de travailler en boucle fermée

Toutes ces propriétés entraînent une utilisation particulière de l’AOP. Le gain étant infini, on n’utilisera jamais l’amplificateur en boucle ouverte car, pour une tension différentielle d’entrée infiniment petite, la tension de sortie serait infinie.

Pour donner une idée de la grandeur, si vous appliquez une tension différentielle de 1 mV (1.10^-3 V) aux entrées, la sortie serait de 200V. Il est bien évident qu'avec une alimentation de 15V, vous ne pourrez obtenir cette valeur, vous atteindrez seulement la tension de saturation plus ou moins égale à l'alimentation.

L’amplificateur serait saturé puisque la tension de sortie ne peut être supérieure à la tension d’alimentation. Nous monterons donc un amplificateur opérationnel en boucle fermée (avec une contre-réaction ou negative feedback). Cette contre-réaction sera soustractive, autrement dit elle se soustraira de la tension différentielle d’entrée, ce qui diminuera cette dernière et maintiendra la sortie dans les limites finies. 

   6.      Ce qui différencie un AOP idéal d'un AOP réel :

En général nous décrivons des éléments parfaits, or chacun le sait rien n'est parfait. Nos AOP présentent des imperfections qu'il convient de connaître. 

6.1.   Tension de décalage en entrée 

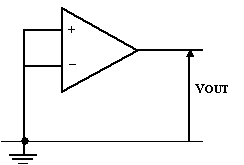
Nous relions nos deux entrées à la masse, VIN=0. On constate qu'il existe en sortie une tension VOUT non nulle. Ceci est du à l'inévitable dissymétrie de construction des entrées. On la compense par un potentiomètre monté sur les broches appropriées (offset) du circuit intégré.

6.2.   Courant de polarisation d'entrée 

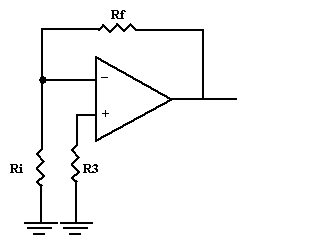
Les entrées de l'AOP sont des transistors qui ont besoin d'être polarisés. Cette polarisation doit être rigoureusement identique pour les deux étages ce qui n'est jamais le cas et provoque des décalages de la tension de sortie. On y remédie en montant sur l'entrée non inverseuse une résistance R3 de valeur : 

  Rf x Ri

R3 = -----------

 (Ri+Rf)

6.3.   Taux de réjection en mode commun CMRR (Common mode rejection ratio) 

Idéalement un AOP n’amplifie que les signaux en mode différentiel et pas en mode commun. Un signal mode commun est un signal qui est appliqué simultanément aux deux entrées, c'est le cas de tous les parasites et autres perturbations. 

L'AOP devrait donc amplifier uniquement en mode différentiel, donc ne pas amplifier ces signaux. Ce n'est pas tout à fait le cas et en sortie on retrouvera un signal amplifié en mode différentiel (ce que nous voulons) et une partie du signal amplifié en mode commun (ce que nous ne souhaitons pas). Le taux entre amplification mode différentiel et amplification mode commun s'appelle le CMRR. Comme ce taux est élevé, il est exprimé en dB. Plus le taux est élevé, meilleur est l'AOP. 

7.      Circuits fondamentaux à amplificateur opérationnel

7.1.   Comparateur

Nous avons vu que l’amplificateur opérationnel devait comporter une boucle de rétroaction pour obtenir une tension de sortie finie. Un AOP non muni d’une telle boucle est un comparateur, c’est-à-dire un composant donnant une certaine tension de sortie si la tension est négative et une autre tension si l’entrée est positive.

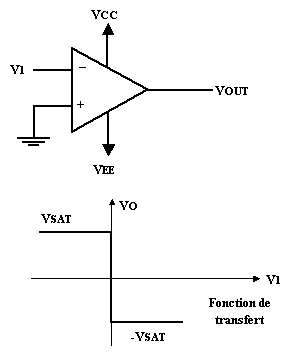
VOUT est la tension de sortie, VIN est la tension d'entrée en mode différentiel (VIN = V1-V2). VSAT, qui est la tension de saturation, est proche de VCC, -VSAT est proche de VEE. Si l'AOP est alimenté par une seule tension Vcc, la caractéristique se trouve amputée de la partie basse qui va de 0 à -VSAT. La zone de fonctionnement linéaire se situe entre les deux valeurs de VSAT. 

En clair le dispositif fonctionnera en comparateur de tension. Si la tension sur l'entrée non inverseuse est supérieure à la tension présente sur l'entrée inverseuse, la sortie bascule au niveau haut proche de VCC. Dans le cas contraire, V2 < V1, la sortie bascule vers le niveau bas soit VEE. Si le circuit  est alimenté par une tension non symétrique comme par exemple (+15, 0V) la sortie aurait basculé vers 0V lorsque V2 < V1.

Si l’entrée non inverseuse n’est pas à la masse mais à une tension VRÉF, les changements d’état se feront à VRÉF.

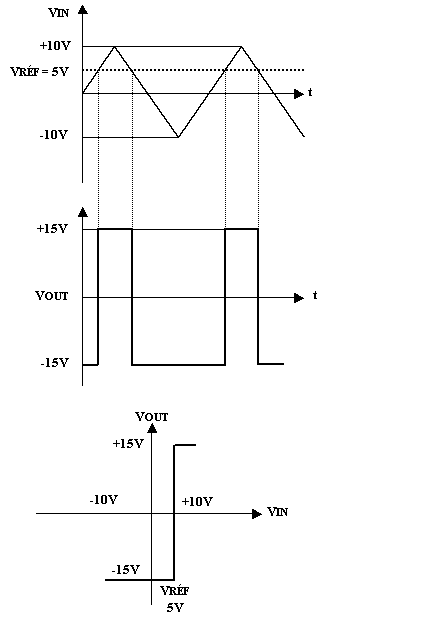
Exemple #1

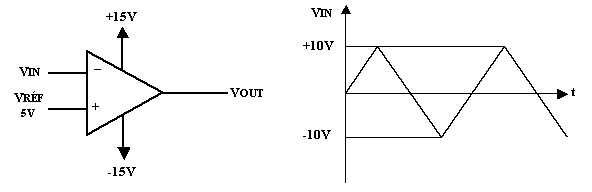
Question :  

a)         Tracer l’onde de VOUT  

b)        Tracer la fonction de transfert 

Solution 

Exemple #2

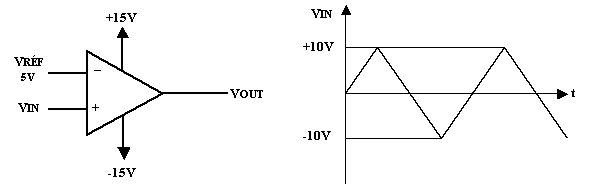
Question :  

c)         Tracer l’onde de VOUT  

d)        Tracer la fonction de transfert   

Solution 

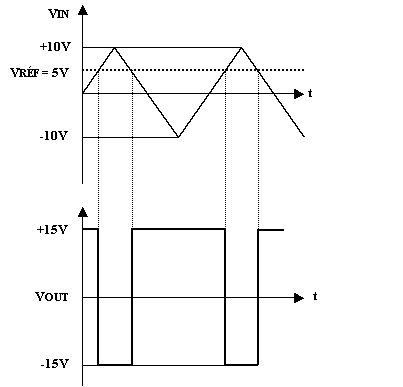
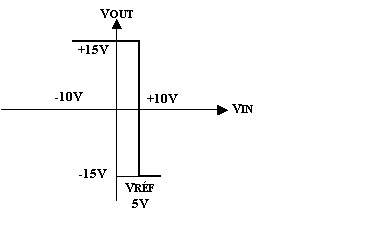
Réponse en fréquence de l'amplificateur opérationnel :

Jusqu’à présent, nous avons supposé que la bande passante, c’est-à-dire la gamme des fréquences dans laquelle on faisait les calculs était infinie. Ceci n’est malheureusement pas les cas. La figure suivante donne l’allure du gain en tension en boucle fermée en fonction de la fréquence. Le gain de 200 000 que l’on prenait en considération n’est valable qu’en continu jusqu’à une fréquence d’environ 6 Hz. Ensuite, il décroît rapidement. Le gain est divisé par 10 lorsque la fréquence est multipliée par 10.  

Si on exprime le gain en décibel sachant que A (dB) = 20 log (VOUT / VIN), on dira qu’il décroît de 20 dB par décade c’est-à-dire qu’il diminue de 20 dB lorsque la fréquence est multipliée par 10. 

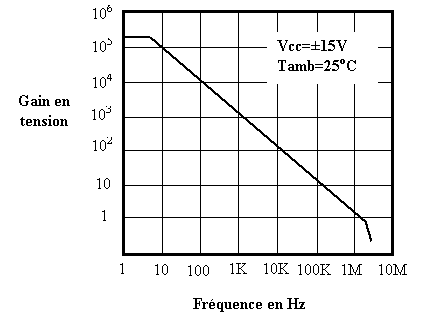
Remarque : le tracé est logarithmique.

·         L'amplification est unitaire à la fréquence de 1 MHz. Ce point remarquable s'appelle Fréquence unité ou produit Gain-Bande Passante noté en anglais GBW (Gain Band Width).

·         Vous mesurez en observant la courbe de réponse du gain en fonction de la fréquence en boucle ouverte combien la contre réaction est vitale et essentielle en électronique.

·         Nous échangerons du gain contre de la bande passante. C'est d'autant plus bénéfique que diminuer le gain augmente la stabilité des amplificateurs et évite les oscillations indésirables.

7.2.   La contre-réaction négative (negative feedback):

Les amplificateurs hélas, n'ont pas la faculté d'amplifier les signaux dans une grande bande passante et avec un gain constant. 

La courbe de réponse d'un amplificateur à composants discrets ressemble à ceci :

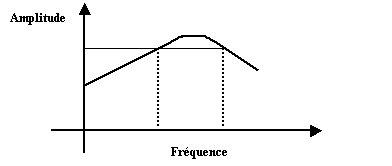
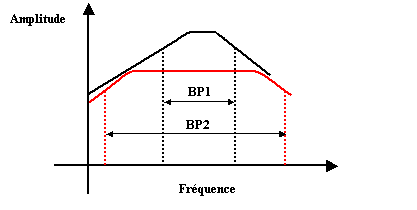
L'idée de base est de réduire le gain de manière à augmenter la bande passante. Ceci est visible sur le dessin ci-dessous. Le trait noir montre une bande passante réduite à fort gain, tandis que le trait rouge laisse apparaître une BP plus large mais avec gain réduit. 

7.3.   Comment faire ?

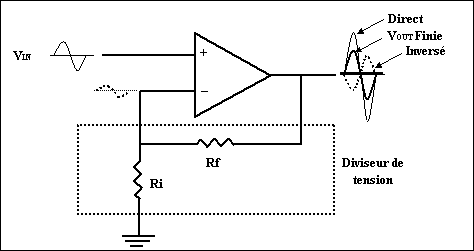
Pour réaliser cela, l'idée est de prélever une partie (faible) du signal de sortie et de la réinjecter à l'entrée de l'amplificateur en opposition de phase naturellement. Les signaux de sortie viendront se soustraire aux signaux d'entrée de manière à faire travailler l'amplificateur dans sa partie linéaire. Ceci conduira à diminuer le gain de l'amplificateur et à augmenter sa bande passante. 

Si nous injections les signaux non pas en opposition de phase (180°) mais en phase nous réaliserions un oscillateur. 

Le signal sera prélevé et injecté par le biais de résistances et c'est en ajustant ces résistances que nous pourrons régler le taux de rétroaction.

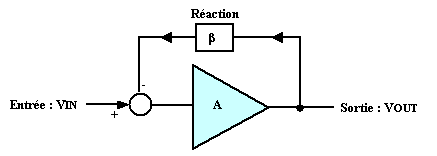
 Voilà le principe : La boucle de réaction peut être négative ou positive. Quand elle est négative, l'ampli est contre-réactionné, quand elle est positive, le montage oscille.

Ce mode de fonctionnement avec contre-réaction sera appelé “mode en boucle fermée”   

A est le gain en boucle ouverte de l’amplificateur (noté souvent AOL “open loop”), et b, le coefficient d’atténuation de la contre-réaction. Si on appelle V’IN l’entrée de l’AOP, alors : 

V’IN = VIN – bVOUT et VOUT = AV’IN   

VOUT  

------ = V’IN = VIN - bVOUT è VOUT = AVIN - AbVOUT è VOUT + AbVOUT = AVIN 

  A   

VOUT (1 + Ab) = AVIN

VOUT             A  

------ = ----------- = ACL (closed loop)  

VIN            1 + Ab   

Le gain en boucle fermée est finie et dépend du coefficient d’atténuation b. Il est beaucoup plus petit que le gain en boucle ouverte  

Exemple : A= 200 000 et b = 0.1 è ACL = 200 000 / (1 + 200 000 x 0.1) = 10 

7.4.   Règles de simplification

On utilise deux petites règles simples pour faire l’analyse du comportement des amplificateurs opérationnels. Celles-ci découlent des caractéristiques idéales données précédemment. 

Premièrement : le gain est tellement élevé qu’une fraction de millivolt entre les bornes d’entrée va faire bouger la sortie sur toute l’étendue possible. Ceci nous amène à ignorer cette petite tension. On dit donc : 

Règle #1 : la sortie va tout tenter pour réduire la tension différentielle d’entrée à zéro. 

Deuxièmement, les amplificateurs opérationnelles ne tirent que des courants très faibles par leurs entrées. Ces courants sont dans l’ordre du nanoampère. On dit donc : 

Règle #2 : les entrées ne demandent aucun courant. 

7.5.   Amplificateur non inverseur à gain fini

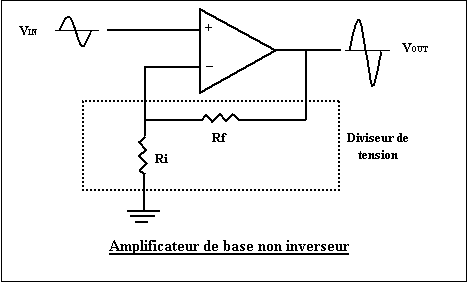
La contre-réaction négative telle qu’illustrée à la figure suivante est la comparaison continuelle de VIN avec VOUT. Via un diviseur de tension on ramène à l’entrée inverseuse une portion du signal électrique présent à la sortie de l’amplificateur opérationnel (VOUT) pour la comparer avec la tension d’entrée (VIN) présente sur l’entrée non inverseuse. On dit alors que le circuit fonctionne en boucle fermée.

7.5.1.      Principe

Un montage non inverseur fournit une tension de sortie en phase avec la tension d’entrée (voir figure précédente). Dans ce circuit, le signal est appliqué à l’entrée non inverseuse (+) de l’amplificateur. Une boucle de contre-réaction, formée par un diviseur de tension (Rf et Ri) ramène une portion du signal de sortie (VOUT) sur l’entrée inverseuse (-). 

La figure suivante illustre comment se calcule le gain d’un amplificateur en boucle fermée. Le gain en tension AV est le rapport entre VOUT et VIN. 

VOUT

Gain = --------

  VIN

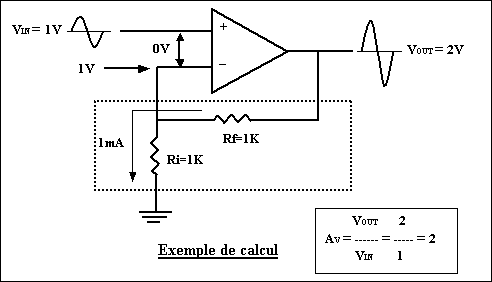
Dans l’exemple de la figure précédente, VIN = 1 volt.

Règle #1 : Vdiff = 0 volt. La tension aux bornes de Ri vaut donc 1 volt et son courant est de 1 mA

Règle #2 : les entrées ne demandent aucun courant. Le courant de 1 mA provient donc de la sortie de l’amplificateur opérationnel. La chute de tension dans la résistance Rf de 1K vaut donc 1 volt.

La sortie de l’amplificateur s’est donc ajustée à 2 volts car VOUT = VRi + VRf = 1V + 1V = 2V 

AV = VOUT / VIN 

VOUT = (Rf + Ri) x I

VIN = Ri x I 

           VOUT       (Rf + Ri) x I        (Rf + Ri)          Rf             Ri             Rf

AV = --------- = -------------- = ------------ = --------+ --------- = ------- + 1

            VIN              Ri x I                  Ri               Ri              Ri             Ri

Un diviseur de tension par 2 produit un gain de 2, un diviseur de tension par 10 produit un gain de 10 etc. 

Exemple   

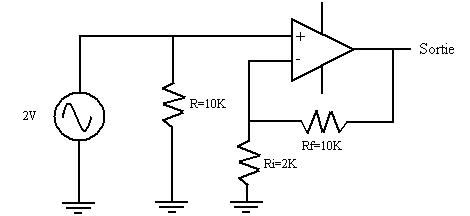
Questions : AV = ?, VOUT = ?, VRi = ? VRf = ? 

AV = (Rf / Ri) + 1 = (10 / 2) + 1 = 6 

VOUT = AV x VIN = 6 x 2 = 12 volts 

VRi = VIN = 2 volts 

VRf = VOUT – VRi = 12 – 2 = 10 V 

7.5.2.      Impédance d’entrée d’un montage non inverseur

On a vu que l’impédance d’entrée d’un ampli opérationnel idéal est l’infini. On peut ainsi ajuster aisément l’impédance d’entrée grâce à une résistance qu’on place entre l’entrée non inverseuse et la masse (à la figure précédente, l’impédance d’entrée qui est R vaut donc 10K). 

Exemple

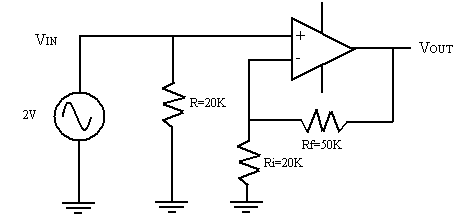
Questions : AV = ?, VOUT = ?, ZIN = ? 

AV = (Rf / Ri) + 1 = (50 / 20) + 1 = 3.5 

VOUT = AV x VIN = 3.5 x 2 = 7 volts 

ZIN = R = 20K 

7.6.         Montage inverseur 

7.6.1.      Principe

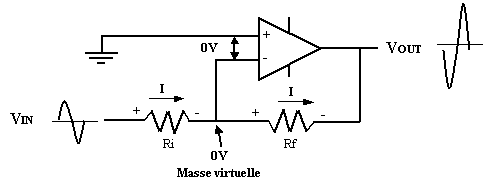
        L’entrée se fait via RIN sur l’entrée inverseuse de l’ampli opérationnel. Noter encore selon la règle #1 que le potentiel à cette entrée est maintenu à 0 V. On l’appelle “point commun virtuel” ou “masse virtuelle”. On retrouve ainsi la tension VIN aux bornes de la résistance RIN et le courant de RIN passe au travers de la résistance RF (règle #2). De là on peut calculer VOUT : 

VOUT = - RF x I

Comme VIN = RIN x I, alors on peut déterminer le gain : 

          VOUT       -RF x I           RF

AV = ------- =  ---------- = - -------

           VIN         RIN x I          RIN 

Le signe moins (-) montre que la sortie est déphasée de 180° par rapport à l'entrée d'où son nom de “montage inverseur”. 

7.6.2.      Impédance d’entrée

L’impédance d’entrée de ce montage est : 

ZIN = VIN / I = RIN x I / I = RIN 

En effet on voit que le courant d’entrée est déterminé par la valeur de RIN. On peut alors dire que la valeur de l’impédance d’entrée d’un montage inverseur est égale à RIN 

Exemple #1

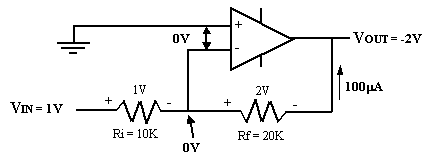
D’un côté de RIN on retrouve VIN à 1 volt et de l’autre côté on retrouve 0 volt (masse virtuelle). Cela crée aux bornes de RIN une différence de potentielle de 1 volt selon les polarités indiquées sur la figure. Le courant  dans RIN est alors de :

I = 1 V / 10 K = 100 mA 

À cause de la règle #2,  tout ce courant traverse RF créant à ses bornes une chute de tension de :

- 100 mA x 10 K = - 2 volts. Cette tension est aussi la tension de sortie.

La tension de sortie a donc dû s’ajuster à – 2 volts de sorte à ajuster la tension différentielle d’entrée de l’amplificateur à 0 volt. 

Vérification : 

AV = - RF / RIN = - 20 K / 10 K = -2

VOUT = AV x VIN = -2 x 1 V = - 2 V 

Exemple #2

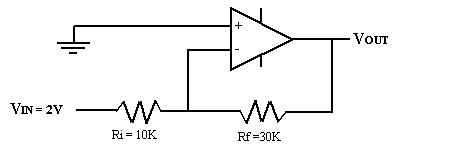
Question

a)                 AV = ?

b)                 VOUT = ?

c)                 ZIN = ?

d)                 VRIN = ?

e)                 VRF = ? 

Solution

a)                  AV = - RF / RIN = - 30K / 10K = -3

b)                 VOUT = AV x VIN = -3 x 2 = -6V

c)                  ZIN = RIN = 10K

d)                 VRIN = VIN = 2V

e)                  VRF = -RF x I = -RF x (VIN / RIN) = - 30K x (2/10K) = -6V 

7.7.     Amplificateur suiveur 

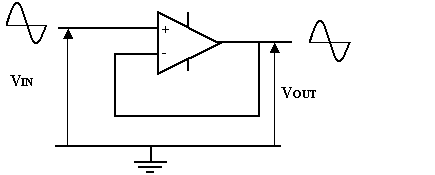
Le gain de cet amplificateur sera égal à l’unité et la sortie sera donc égale à l’entrée. Ce montage apparemment inutile est pourtant très utilisé pour adapter les impédances. On a alors un amplificateur tampon ou intermédiaire (buffer) à impédance d’entrée très élevée et à impédance de sortie basse. 

7.8.     Amplificateur sommateur ou additionneur 

Ce montage hormis ses applications mathématiques est utilisé pour mélanger plusieurs signaux sur un seul amplificateur. En ajoutant un potentiomètre à l'entrée on peut doser le volume pour chaque entrée. Il peut aussi être utilisé comme convertisseur numérique-analogique.

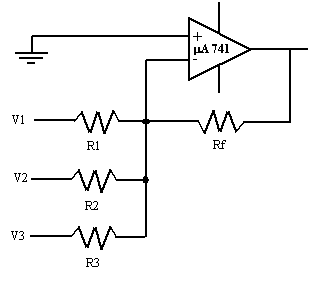
Selon la règle #1, l’entrée inverseuse est une masse virtuelle. Le courant dans R1 est alors égal à V1/R1, celui dans R2 est V2/R2 et celui dans R3 est V3/R3 

Selon la règle #2, Le courant circulant dans Rf est la somme des courants provenant de R1, R2 et R3. 

On peut alors écrire VOUT = - Rf x I = - Rf x (I1 + I2 + I3) 

           V1        V2       V3

VOUT = - Rf ( ----- + ------ + -------)

           R1        R2       R3 

Si on prend Rf = R1 = R2 = R3, alors : 

VOUT = - (V1 + V2 + V3), d’où le nom de sommateur donné à ce montage. 

Exemple : Soit le montage ci-dessus où Rf = R1 = R2 = R3 = 10 K, V1 = 1 V, V2 = 2 V, V3 = 3 V. Calculer :

a)                  IR1

b)                 IR2

c)                  IR3

d)                 IRf

e)                  VRF

f)                   VOUT 

Solution :  

a)                  IR1 = V1 / R1 = 1 / 10 K = 100 mA

b)                 IR2 = V2 / R2 = 2 / 10 K = 200 mA

c)                  IR3 = V1 / R1 = 1 / 10 K = 300 mA

d)                 IRf = IR1 + IR2 + IR3 = 100 mA + 200 mA + 300 mA = 600 mA

e)                  VRF = -Rf x IRF = -10K x 600 mA = -6V

f)                   VOUT = VRF = -6V 

7.9.     Amplificateur soustracteur

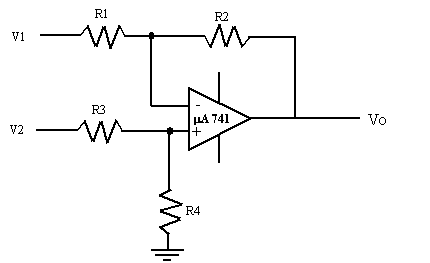
Puisque l’impédance d’entrée de l’AOP est infinie, aucun courant n’y entre. Le courant qui circule dans R1 parcourt donc R2, et celui qui circule dans R3 parcourt donc R4. De plus, le gain en boucle ouverte étant infini, la tension différentielle à l’entrée de l’AOP est pratiquement nulle. Les deux entrées ont donc le même potentiel. Appelons V cette tension commune aux deux entrées. On a alors : 

 V1 – V      V- VO

--------- = --------

     R1           R2 

et 

 V2 – V          V

--------- = --------

     R3            R4

 V2          V             V           V(R3+R4)

------ = ------- + -------- = ------------

 R3         R3           R4            R3 x R4

         V2 x R4

V = -------------

         R3 + R4 

 V1        V          V        VO

------ - ------ =  ----- - -------

 R1          R1       R2       R2   

 V1         VO         V          V            V(R1+R2)             V2 x R4(R1+R2)

------ + ------ = ------ + ------- = -------------- = ------------------------

 R1          R2       R2         R1             R1 x R2           (R3 + R4) x R1 x R2 

   VO         V          V            V(R1+R2)            V2 x R4(R1+R2)            V1

 ------ = ------ + ------- = -------------- = -------------------------- - -----

   R2        R2         R1           R1 x R2             (R3 + R4) x R1 x R2          R1   

              V2 x R4(R1+R2)R2           V1 x R2

 VO  = -------------------------- - ------------

              (R3 + R4) x R1 x R2              R1 

Si on prend R1=R2=R5 et R3=R4=R6, alors : 

              V2 x R6(2R5)R5           V1 x R5

 VO  = ---------------------- - ------------ = V2 – V1

               2R6 x R5 x R5                 R5   

La tension de sortie est égale à la différence des deux tensions d’entrée. D’où le nom de soustracteur donné à ce montage.

Exemple : Soit le montage ci-dessous où R1 = R2 = R3 = R4 = 10 K, V1 = 3 V, V2 = 4 V, V3 = 3 V. Calculer :

a)                  VOUT

b)                 VA

c)                  VB

d)                 VR1

e)                  IR1 

f)                   IR2

g)                  VR2

h)                  VOUT

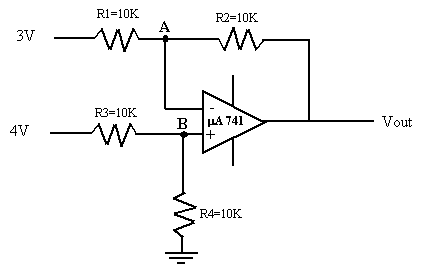
Solution : 

e)         VOUT = V2 – V1 = 4 – 3 = 1 volt

f)          VB = 4V /2 = 2 volts

g)         VB = VA = 2 volts

h)         VR1 = V1 – VA = 3 – 2 = 1 volt

i)           IR1 = VR1 / R1 = 1 / 10K = 100 mA

j)          IR2 = IR1 = 100 mA

k)        VR2 = IR2 x R2 = 100 mA x 10K = 1 volt

l)           VOUT = VA – VR2 = 2 – 1 = 1 volt 

8.      Amplificateur de courant pour amplificateur de tension

Le courant maximal de sortie d’un amplificateur opérationnel typique est limité. Pour un UA741, par exemple, il est de 25 mA. Si la charge exige un courant plus élevé, il faut ajouter un élément “amplificateur de courant” à la sortie. Le circuit suivant l’illustre bien.

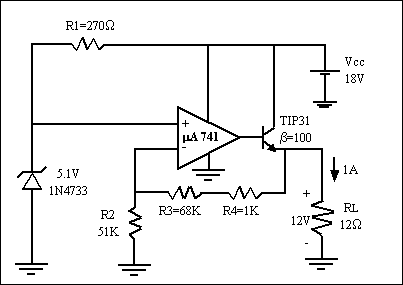
L’AOP donne le courant IB qui contrôle IC et IE. La charge est alimentée par l’émetteur d’où sort ce courant IE.   

Ce circuit illustre bien le rôle du transistor. L’amplificateur ne peut fournir lui-même le courant de 1 ampère exigé par la charge de 12 watts. Le transistor vient donc à sa rescousse en lui fournissant les muscles manquants. L’amplificateur ne fournit que 10 mA (1A/b=1A/100=10mA), ce qu’il est en mesure de faire. 

• Retour à semi-conducteurs
  
• Sommaire
  
• Accueil